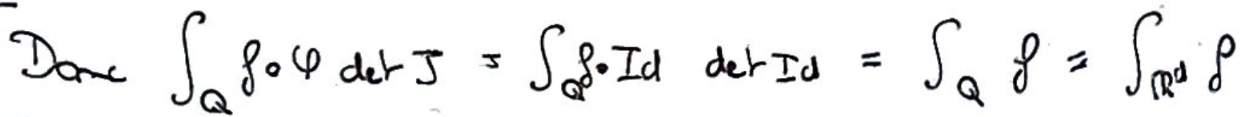Lemme de Lax - Math'φsics

Lemme de Lax

Formulaire de report
Problème d'affichage Contenu de la note peu pertinent
Lemme de Lax :
\(\varphi\in\mathcal C^2({\Bbb R}^d,{\Bbb R}^d)\)

\(\varphi\) est telle que \(\varphi(x)=x\) pour tout \(x\in{\Bbb R}^d\setminus B^\prime(0,1)\)

\(f\in\mathcal C_c^\infty({\Bbb R}^d,{\Bbb R}^d)\)

$$\Huge\iff$$

$$\int_{{\Bbb R}^d}f(z)\,dz=\int_{{\Bbb R}^d}f\circ\varphi(x)\operatorname{det}(J(x))\,dx$$
Démonstration du théorème de Lax en dimension \(2\) :

On borne le support de \(f\), et on pose \(g\) une primitive par rapport à sa première variable.

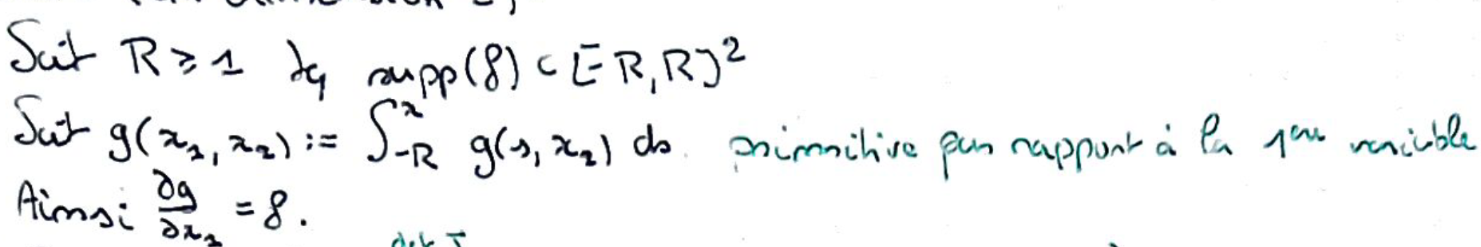
On joue avec la Règle de la chaîne pour simplifier l'expression de \(f\circ \varphi\times\lvert J\rvert\).

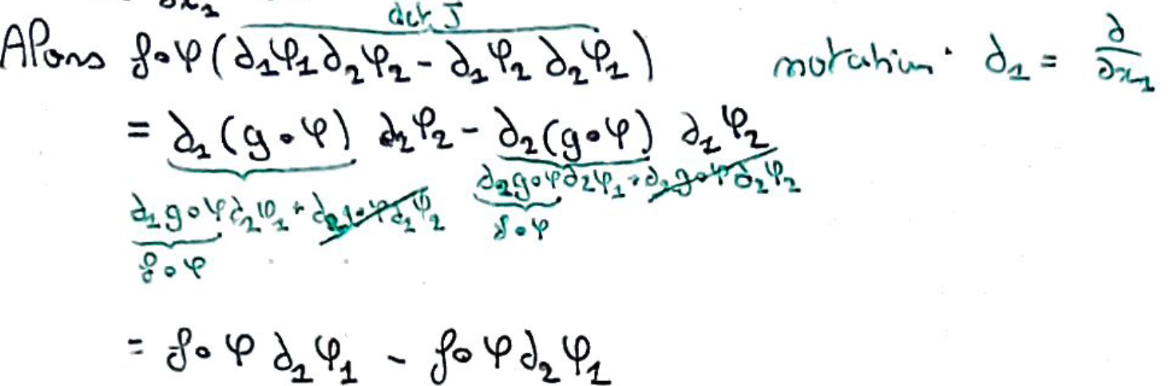
L'intégrale est donc en deux parties : l'une qui ne dépend que des valeurs sur le bord et l'autre qui s'annule via le Théorème de Schwarz.

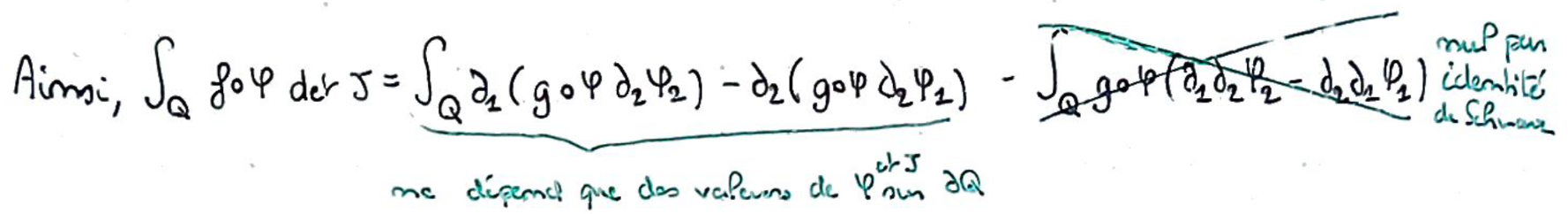
On peut donc remplacer \(\varphi\) et \(J\) par \(\operatorname{Id}\), ce qui nous donne l'égalité recherchée.